La distribuzione log-normale è una distribuzione continua, monomodale, asimmetrica, nella quale moda, mediana e media non coincidono.
L’espressione analitica della PDF (Probability Distributive Function) è
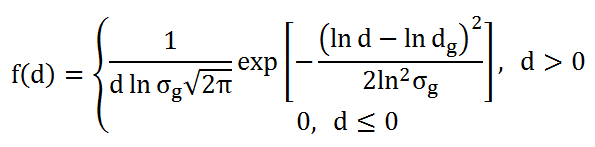
dove d è il diametro aerodinamico, dg è la media geometrica e σg è la deviazione standard geometrica.
Il campo di esistenza di questa funzione è l’intervallo infinito 0<d<+∞.
La funzione f(d) è normalizzata perché soddisfa la condizione
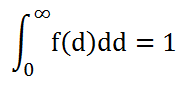
La media geometrica è data da
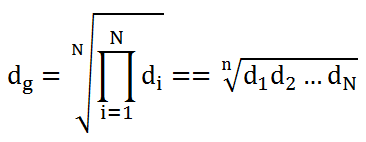
La deviazione standard geometrica è data da
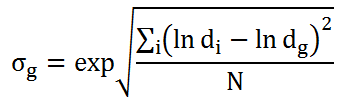
Il grafico di questa distribuzione è
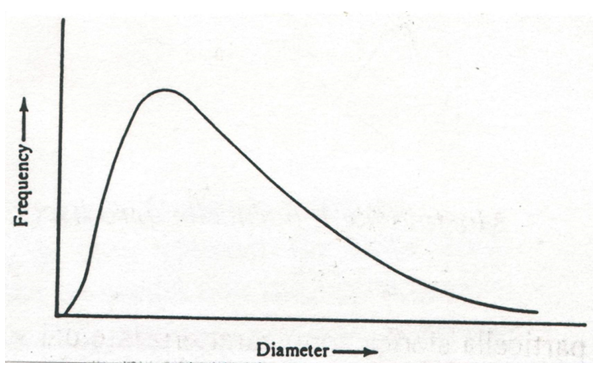
Si può dimostrare che il 68.27% delle dimensioni dei diametri delle fibre cade nell’intervallo dg∙σg e dg⁄σg.
Ponendo x= lnd si ottiene una distribuzione normale o gaussiana la cui PDF è
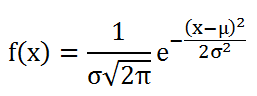
La distribuzione normale è simmetrica rispetto a x=μ (moda, mediana e media coincidono). Il campo di esistenza della funzione di Gauss è -∞<x<∞.
Il grafico di questa funzione è
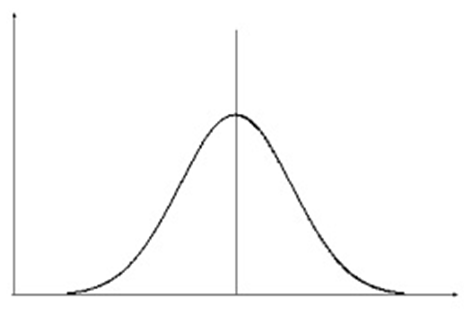
Anche la funzione di Gauss è normalizzata
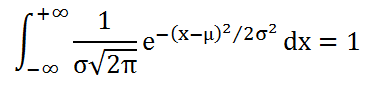
Le caratteristiche numeriche di posizione di una distribuzione sono:
- speranza matematica;
- moda;
- mediana;
- quartili, decili, centili (o percentili).
La caratteristica principale di posizione è la speranza matematica o valor medio che, nel caso di una distribuzione continua, è data da
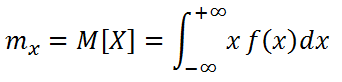
dove X è una variabile aleatoria continua.
La moda è quel valore che si verifica il maggior numero di volte o, in altre parole, che ha la maggior probabilità di verificarsi. Per questo valore di x, f(x) ha un massimo.
La mediana è quel valore per cui
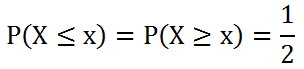
La mediana corrisponde a quel valore di x che separa la curva di distribuzione in due parti, ciascuna con area pari a ½.
Altri indici di posizione sono i quartili, i decili e i centili ( o percentili).
È spesso conveniente suddividere l’area sotto la curva di distribuzione in modo tale che l’area a sinistra di xα sia una qualche percentuale dell’area totale unitaria. I valori corrispondenti a tali aree sono detti valori percentili o percentili. Così l’area a sinistra di xα è α:
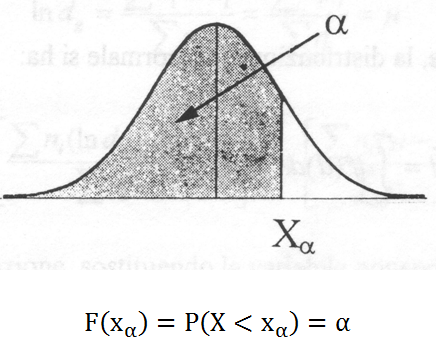
La funzione di distribuzione cumulativa (CDF, Cumulative Distribution Function) è definita come la probabilità che la variabile aleatoria X assuma un valore inferiore a x, questa probabilità è data da:

Il valore centrale è la mediana. Analogamente si possono individuare altri indici di posizione. Nel caso della distribuzione log-normale il 16°, il 50° e l’84° percentile sono rispettivamente dg⁄σg , dg e dg∙σg.
Le caratteristiche numeriche di dispersione dei valori, attorno alla speranza matematica, sono:
- varianza;
- scarto quadratico medio.
La varianza di una variabile aleatoria continua è data per definizione da
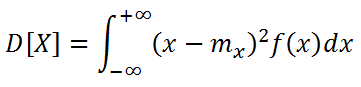
Si chiama scarto quadratico medio della variabile aleatoria X la radice quadrata della sua dispersione
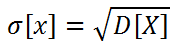
Le distribuzioni spesso non sono simmetriche attorno al loro massimo ma possono avere una delle loro “code” più lunga dell’altra. Le distribuzioni possono essere asimmetriche a destra o a sinistra. Per determinare l’asimmetria di una distribuzione si calcolano dei coefficienti uno dei quali è
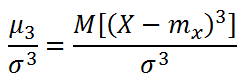 Per la misura del cosiddetto appiattimento, cioè dell’acutezza o della piattezza della distribuzione, si calcolano dei coefficienti di appiattimento (o curtosi) come il seguente
Per la misura del cosiddetto appiattimento, cioè dell’acutezza o della piattezza della distribuzione, si calcolano dei coefficienti di appiattimento (o curtosi) come il seguente
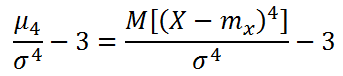
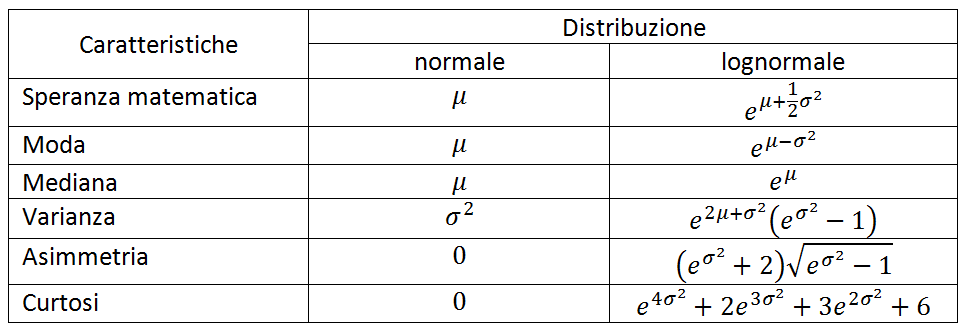
Nella tabella seguente sono riportate le principali caratteristiche delle distribuzioni normale e log-normale:
La moda è quel valore che si verifica il maggior numero di volte o, in altre parole, che ha la maggior probabilità di verificarsi. Per questo valore di x, f(x) ha un massimo.
La mediana è quel valore per cui


